Introducción
Los
mitos y leyendas durante siglos han rodeado al arco iris y en muchas
partes del mundo han jugado un gran rol en las creencias de la gente.
Para muchas culturas occidentales el arco iris fue visto como un
puente entre el cielo y la tierra. La brillantez de los colores en un
arco iris tiene significado, un verde prominente significa
abundancia, el rojo significa guerra y el amarillo significa que la
muerte está en camino.
Uno
de los mitos más extraños sobre los arco iris es la idea que una
olla con oro se podría encontrar al final de un arco iris (dejada
por duendes o hadas). Otra leyenda antigua europea dice que el que
pase bajo un arco iris sería transformado de hombre en mujer y de
mujer en hombre.
Pero,
¿qué es un arco iris? Una respuesta puede ser “ un arco brillante
de colores que aparece en el cielo cuando el sol brilla durante o
poco después de una lluvia".
Esta
respuesta, simplifica en extremo los numerosos procesos científicos
que se combinan para producir lo que podría llamarse una de las
muestras más espectaculares de la naturaleza.
A
continuación se presenta la explicación científica de este
fenómeno.
La
teoría de Descartes
René
Descartes, famoso científico francés, realizó el primer trabajo
formal sobre arco iris alrededor de 1637. Él dijo que para que se
forme un arco iris, se deben cumplir dos condiciones. La primera es
que la fuente de luz (generalmente el sol) debe estar directamente
detrás del observador y la segunda es que el cielo enfrente del
observador debe estar lleno con humedad. Descartes también cayó en
cuenta que las gotas de agua en la lluvia eran la clave para la
formación del arco iris, simplifica el estudio reduciendo su
investigación a una sola gota de agua, para analizar como interactúa
con la luz, Descartes escribió “considerando que el arco no solo
aparece en el cielo sino también en el aire cercano a nosotros,
cuando hay gotas de agua iluminadas por el sol, como se ve en ciertas
fuentes. Yo pensé que se forman solo de la manera como el rayo de
luz actúa sobre estas gotas y pasa de ellos a nuestros ojos. Mas aun
sabiendo que las gotas son redondas, y viendo que hay grandes y
pequeñas, la apariencia de un arco no cambia de ninguna forma, esto
me dio la idea de hacer una muy grande, tal que pudiera examinarla
mejor”.
 |
Figura 1 El experimento de Descartes.
|
Descartes
sostuvo una esfera grande llena con agua frente a la luz solar y miró
sus rayos reflejados. (Figura 1). Observó que si sus ojos se sitúan
en el punto Z, con “ la luz del sol “ viniendo de A y E.
Sosteniendo la esfera de agua arriba en la posición BCD, el punto D
aparece rojo y más brillante que el resto de la esfera. También
observó que si se acercaba o alejaba de la esfera, a la izquierda o
derecha, o aun rotando su cabeza alrededor de ella. Como la línea DE
siempre forma un ángulo de 42o
con la horizontal el punto D siempre aparece rojo, pero al momento
que el ángulo DEF se agranda, el color desaparece y si se hace al
ángulo menor, el color rojo en D parecerá dividirse en un numero de
colores menos brillantes.
 |
Refracción & Reflexión de una gota de agua
Figura 2
|
El
experimento de Descartes explica en cierta forma la formación del
arco iris. Determina que un rayo de luz monocromática debe entrar a
la superficie frontal de la gota donde se refracta debido al paso de
la luz entre dos medios diferentes. Una vez dentro de la gota el rayo
de luz continúa en línea recta hasta que se encuentra con la
superficie posterior de la gota, donde se refleja y sale nuevamente
en línea recta hasta que llega a la superficie frontal, donde
nuevamente se refracta (figura 2).
Descartes
matemáticamente trazó una serie de rayos paralelos a través de una
gota de agua esférica, porque conocía la ley de refracción y
reflexión pudo calcular la trayectoria completa del rayo de luz
entrando y saliendo de una gota simple, la cual ha sido reflejada y
refractada internamente,
 |
Angulo de arco iris
Figura 3
|
La
figura 3 muestra las trayectorias que calculó Descartes y muestra
claramente que un rayo que entra en una gota por el centro de su
superficie frontal se reflejará a lo largo de su trayectoria
incidente (referido frecuentemente como eje de la trayectoria)
De
esta investigación Descartes encontró que más rayos emergen entre
41o
y 42o que
en otro intervalo y que el ángulo del rayo de Descartes era
alrededor de 41.6o,
Note que es solamente un ángulo aproximado, como el ángulo real
depende del color en consideración. Todos los ángulos indicados son
para el componente rojo, salvo se establezca otra cosa.
Propiedades
de la luz
¿Qué es la luz? La luz se
considera generalmente como una onda. Los detalles de tales ondas son
difíciles de describir, tal que primero introduzcamos algunos
conceptos para ondas de agua (más fáciles de visualizar) y luego
generalizarlas para ondas de luz.
Si
sueltas una piedra en un lago podrás ver ondas circulares que se
mueven hacia afuera desde el punto donde la piedra golpeo la
superficie. A una velocidad fácil de medir (v). La distancia entre
la parte mas alta (cresta) de una onda a la parte mas baja de la
siguiente se refiere a la longitud de onda (.
Consideremos que hay un poste en el agua, cuando las ondas pasan es
posible cronometrar el tiempo que toma entre la llegada de una
cresta y otra. (T). La razón con la que están pasando estas crestas
es 1/T, conocida como la frecuencia de la onda (f). Obviamente estas
tres cantidades están relacionadas por una ecuación, v es igual a
multiplicado
por f. Todas las ondas (incluyendo las ondas de luz) están
caracterizadas por estas cantidades. La luz es una onda, pero ¿cuál
es su velocidad?
En
el vacío, la luz viaja a 300 000 000 metros por segundo. ¿Cuál es
su frecuencia? Aquella que determina cual es el color de luz que
percibimos. La luz roja tiene una frecuencia, la luz amarilla una
frecuencia más alta, la luz violeta tiene una frecuencia mayor. De
hecho ondas con frecuencia menores que la roja y mayores que la
violeta existen, nuestros ojos no son capaces de detectarlas. ¿Cuál
es la verdadera frecuencia de la luz blanca? Realmente la luz blanca
esta compuesta de una mixtura de todos los colores de la luz
visible, esto nos da una pista de que el arco iris tiene las
diferentes frecuencias y de ese modo podría ser originado a partir
de la luz blanca.
Antes
de ir a discutir a mayor profundidad el arco iris. Es importante
cubrir tres tópicos de la física. Los tres tópicos son
reflexión, refracción y la ley de snell.
Refracción
Hay
dos leyes que gobiernan la refracción y ellas son:
Cuando
un frente de ondas (sea luz o sonido) se mueve entre dos medios, con
diferentes densidades ópticas hay un cambio en la velocidad de la
onda, que da como resultado la alteración de la dirección de onda.
Este cambio en la dirección de la onda se conoce como refracción y
la dirección en la cual la onda es refractada depende de sí el
segundo medio es de mayor o menor densidad óptica que el primer
medio (Figura 4).
El
rayo incidente, el rayo refractado y la normal a la superficie
entre los dos medios descansan sobre un mismo plano. Las tres se
encuentran en el límite entre los dos medios en un punto llamado
punto de incidencia. (Figura 4).
 |
Límite de refracción
Figura 4
|
La ley de
Snell
Conocida por algunos como ley
de Descartes, debido a que René Descartes descubrió la relación al
mismo tiempo que snell establece lo siguiente.
El
seno del ángulo entre el rayo en el primer medio y la normal es
igual a una constante por el seno del ángulo entre el rayo en el
segundo medio y la normal. Por consiguiente la constante depende
solamente de las densidades ópticas de los medios en contacto,
constante conocida como índice de refracción.
Reflexión
La
reflexión es el cambio de dirección cuando un frente de ondas
rebota de una superficie.
El
rayo incidente, el rayo refractado y la normal, todas están en un
mismo plano y se encuentran en el límite entre los dos medios en un
punto simple llamado punto de incidencia.
El
ángulo de incidencia (i) = el ángulo de reflexión(r)
Los
colores del arco iris
 |
Longitudes de onda
Figura 5
|
Tradicionalmente
los colores que forman el arco iris, se describen como siete colores,
Rojo, Naranja, Amarillo, Verde, Azul, Índigo, y Violeta. En
realidad el arco iris esta formado por de un espectro de todos los
colores del rojo al violeta y más allá del ultravioleta y del
infrarrojo, cuales no son detectables por los ojos (ver figura 5).
Cuando este espectro se combina aparece blanco a loa ojos, fenómeno
que fue demostrado por Sir Isaac Newton en 1666.
Cuando
un rayo de luz entra a la gota se refracta. Sin embargo no toda la
luz se refracta la misma cantidad, resultando en una dispersión de
colores como un prisma (Figura 6). La componente roja se desvía
menos y la componente violeta se desvía mas que cualquier otro
color. Los diferentes colores se desvían diferentes cantidades
porque los colores tienen frecuencias diferentes (Tabla 1) luego
viajan a velocidades diferentes en materiales transparentes. Debido a
que viajan a diferentes velocidades, se refractan a diferentes
valores. Si la luz se desvía dos veces como en un prisma, la
separación de colores es muy notoria. Esta separación de colores se
conoce como dispersión.
Tabla
1(Frecuencia de los diferentes colores)
Color
Límite bajo (nm) Límite alto (nm)
 |
Prisma Figura 6
|
Rojo 635 665
Naranja 600 635
Amarillo 565 600
Verde 495 565
Azul 445 495
Violeta 420 445
Como
se establece arriba los colores del arco iris están en el espectro
entero de colores del rojo al violeta y mas allá. Si embargo para
simplificar la explicación del arco iris se muestra como formado
por bandas, los colores que se consideran en esta discusión son los
siete tradicionales.
Miles
de pequeñas gotas esféricas de agua pueden actuar como prismas,
descomponiendo la luz en sus diversos colores.
.
A
pesar que cada gota de agua dispersa el espectro total de colores, un
observador estará en posición de ver solamente un solo color de una
gota en particular (Figura 7). Si la luz violeta de una gota de agua
alcanza el ojo de un observador, la componente roja de la gota
incidirá en otro lugar (hacia los pies del observador). Para ver la
componente roja, el observador necesitaría ver mas arriba en el
cielo.
Este
hecho da luces sobre algo muy importante de los arco iris, para que
un observador vea un arco iris debe haber muchas (quizás decenas o
cientos de millones) de gotas de agua en la atmósfera. Donde cada
color que llega a los ojos del observador viene de una gota
diferente.
 |
Ángulos de los colores Figura 7
|
Punto
antisolar
Cuando
se discuten los ángulos, que hacen los rayos es usual tomar estos de
una línea imaginaria que va del sol al punto antisolar. Cuando un
observador mira al cielo para ver un arco iris, la luz que entra a la
gota de agua y se refleja la vemos a un ángulo de 42º con la
dirección de la "recta posterior", para poder clarificar
que queremos decir por dirección de la recta posterior consideremos
un rayo que vuelve a lo largo del eje, este estaría en la dirección
opuesta al sol. Este punto directamente opuesto al sol para el
observador, es llamado el punto antisolar. Si el sol estuviera sobre
el horizonte, entonces el punto antisolar estaría debajo del
horizonte. Es interesante notar que la posición del punto antisolar
está marcada por la posición de la parte más alta de la cabeza
del observador en la sombra que éste forma.
 |
Punto antisolar Figura 8
|
Forma
del arco iris
¿Porqué
una gota de lluvia dispersa la luz para formar un arco? La
respuesta a la pregunta involucra el uso de algo de geometría
simple. El primer punto a notar es que el arco iris no es un arco en
dos dimensiones, de hecho es un cono tridimensional con el ápex en
los ojos del observador. La razón por la que parece ser solamente un
objeto bidimensional plano es la misma razón por la que los fuegos
artificiales esféricos en el cielo aparecen en la forma de disco, lo
cual es porque no hay evidencia de distancia. Todas las gotas, que
dispersan la luz hacia el observador están en la forma de un cono
con muchas capas diferentes. Las capas exteriores dispersan la
componente roja, la capa debajo de ella la componente naranja y
luego la amarilla etc. En realidad hay muchas capas, las cuales
dispersan el espectro de colores incluyendo aquellos fuera del rango
del ojo humano (450 – 750 nm).
Para
poder examinar esto consideremos solamente la dispersión de la
componente roja de la luz. Se mostró previamente que la componente
roja se ve con el ángulo entre los rayos incidentes y dispersados
forma un ángulo de 42º. Por supuesto los haces son dispersados a
42º de las gotas de todo el cielo en todas las direcciones hacia
arriba, abajo, izquierda y derecha. Sin embargo la luz roja que llega
a los ojos del observador viene de las gotas de agua que están
sobre el cono que forma un ángulo de 42º, esto es donde el ángulo
entre la línea de incidencia (cual está en la dirección
antisolar) y el borde del cono hace un ángulo de 42º.
 |
Cono de arco iris Figura 9
|
Si
el ojo del observador esta en el ápex del cono como se muestra en la
figura 9, entonces para ver la parte violeta del arco necesitará
mirar a 40º del eje cónico. Luego, el cono que produce la
componente violeta viene de un cono interior a aquel que produce la
parte roja. Un argumento similar se puede hacer para todos los
colores y, porque los colores diferentes se forman por diferentes
conos, entonces cuando ellos se ven del ápex aparecen en forma de
arco.
Nuevamente
se consideran los siete colores tradicionales. Porque
solamente las gotas sobre el cono con ápex en los ojos del
observador son las responsables de la formación del arco iris que ve
el observador, entonces una implicación importante es que cada
persona que mira un arco iris estaría mirando un arco iris
diferente.
Esto
significa que cada persona ve su propio arco iris y nunca dos
personas ven el mismo arco iris porque sus ojos no pueden ocupar el
mismo espacio al mismo tiempo.
Otra
consecuencia es que no hay referencias de distancia un observador lo
ve siempre a ángulos rectos. Cuando se mueve las gotas que forman el
arco iris este cambia. Porque hay un cono diferente de gotas con un
ápex en sus ojos el arco iris también parece moverse con ellos. Sin
embargo de hecho es un arco iris diferente el que ahora vería el
observador. Tal que es imposible ver el costado de un arco iris como
puede sugerir la figura 9.
Todo
este artículo se ha referido al arco iris como un arco o un
semicírculo. Sin embargo, la figura 9 y la discusión anterior
habrían indicado que un arco iris está formado por la luz reflejada
de un circulo de gotas sobre un cono a una distancia común al
observador, incluyendo los del fondo, de allí que un arco iris
completo es realmente un círculo total. ¿Entonces porqué solamente
vemos un semicírculo? La razón es simplemente que el suelo impide
la formación total, debido al hecho que la luz del sol no puede
reflejarse en la tierra húmeda. Sin embargo, si uno estuviera en un
aeroplano o en una montaña alta cuando se forma un arco iris,
permitido por cubierta de nubes será posible ver casi un círculo
completo.
Tamaño
del arco iris
Hasta
ahora se ha discutido el tamaño de un arco iris en términos de su
tamaño angular. Esto no lleva a preguntar “¿Cuán grande es un
arco iris en centímetros, metros o kilómetros? “. La razón
para discutir el tamaño de un arco iris en términos de tamaño
angular y no de su distancia a un observador es que resulta claro
por lo antes visto que el tamaño angular de un arco es el mismo ya
sea que esté formado cercanamente por una fuente de jardín o a
muchos kilómetros por una lluvia. Esto es la parte roja del rayo
siempre se ve a 41,6o
y la violeta a 45o
al punto antisolar.
Debido
a que un arco iris se forma de todas las gotas sobre la superficie
del cono que se acerca o aleja del observador el tamaño del arco
iris no se alterará. De aquí la expresión “buscando una olla con
oro al final del arco iris”, cuyo significado es perseguir algo
que no se puede alcanzar.
Si
no hay forma de alcanzar un arco iris entonces solamente es posible
verlo de un solo lado.
Este
hecho puede verificarse examinando las condiciones necesarias para
la formación de un arco iris, las cuales establecen primeramente que
debe haber humedad en la atmósfera y en segundo lugar que la fuente
de luz debe estar detrás del observador, luego si alguien trata de
ver el otro lado de un arco iris necesitaría estar al otro lado de
las gotas de agua. De tal manera que la fuente de luz estaría
enfrente de él, incumpliendo la segunda condición, más aún si
pudiera ver un arco iris estando al otro lado de las gotas de agua
claramente no estaría viendo el mismo arco iris.
Los
arco iris secundarios
 |
Luz para arcos primario y secundario
Figura 10
|
La
discusión, hasta ahora se ha centrado en el arco iris formado por
reflexiones simples internas dentro de las gotas de agua, que dan
como resultado la formación del arco iris llamado " arco iris
primario ". Sin embargo no son los únicos arco iris formados,
frecuentemente se producen arco iris secundarios.
La
física detrás de la formación del arco iris de segundo orden es
idéntica a la del arco iris primario, excepto que los rayos que
forma son reflejados internamente dos veces dentro de la gota de
agua. Esto lleva a que los arco iris secundarios sean más tenues que
el primario, como una pequeña proporción del rayo es refractada
dos veces dentro de la gota. También lleva a que los colores sean
invertidos, esto es yendo del violeta afuera al rojo adentro. El
tercer efecto de esta doble reflexión interna es que el ángulo al
cual la visión del arco iris secundario no es a 42º como en el
arco primario es aproximadamente a 52º para la componente roja a
aproximadamente 54.5º para la componente violeta del arco (figura
10).
 |
| El arco iris secundario |
Como
se establece arriba un observador solamente "ve" los rayos
particulares que alcanzan sus ojos. La figura 10 muestra dos gotas,
una de las cuales contribuye al arco primario y la otra al arco
secundario, ambas gotas tienen rayos simples y dobles refractados,
pero el diagrama solamente muestra los rayos que llegan a los ojos
del observador.
Arco
iris de alto orden
Así
como dependiendo de su reflexión interna, una sola vez es arco
primario y dos veces es arco secundario, es posible para la luz ir a
tres o más reflexiones internas. Por consiguiente, sería razonable
asumir un arco terciario más tenue mas allá del arco secundario
y aún más tenue arco cuaternario más allá del terciario y así
sería visible.
En
teoría los arcos de alto orden existen, Newton sugirió que toda luz
saliendo de la gota después de tres reflexiones internas sería
demasiado tenue para verla.
R.
Boyer en su libro dice que Jean Bernoulli un contemporáneo de Newton
sugirió que un arco terciario sería visible para las águilas o
linces pero no para los humanos.
De
todos los científicos, Halley (el del cometa famoso) parece haber
sido el primero en realizar cálculos del arco terciario, con
resultados sorprendentes. Halley calculó que el tercer arco tiene un
radio angular de aproximadamente 319.77º, por consiguiente no
aparecería en la parte del cielo opuesta al sol, sino como una
circunferencia alrededor del sol mismo (Figura 11). Por al menos
durante dos mil años el hombre ha estado buscando el arco en la
parte equivocada.
 |
| Figura 11 |
Esto
implica que la razón para que un observador no pueda ver un arco
terciario, no es debido a que es muy tenue como sugirieron Newton y
Bernoulli, sino debido al hecho a que está situado cerca al sol,
donde el cielo es más brillante llegando a cubrir al arco. El
también determina el ángulo del arco cuaternario, esto es el
formado por la cuarta reflexión interna dentro de las gotas.
Halley
encontró que el arco de cuarto orden sería visto con un radio
angular de 314º (Figura 11), nuevamente alrededor del sol y que
después de cinco reflexiones internas, era dudoso que el arco iris
resultante podría ser visto por las águilas o linces.
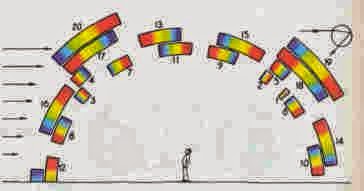 |
Posición de los arco iris de diversos ordenes en el cielo
Figura 12
|
 |
Aparato de Jearl Walker para observar los arco iris en una gota de agua
Figura 13
|
Jearl Walker, famoso
articulista de la revista Scientific American, en el laboratorio
usando un haz láser para iluminar una gota de agua simple (Figura
13), ha testificado aparentemente todos los arco iris hasta el orden
trece, y los ha encontrado en aproximadamente en las posiciones
determinadas por Descartes y Newton.
Sin
embargo, debido a las razones dadas arriba es improbable que los arco
iris de orden mayor a dos puedan ser vistos naturalmente. Habiendo
dicho esto Robert Greenler en su libro reporta que mucha gente dice
haber testificado arco iris de mayor orden, Greenler en sugiere que
ellos deben haber visto porciones de un arco reflejado, observando
arcos de interferencia (ambos discutidos mas adelante), o
también posiblemente debido a sus malas observaciones.
Sin
embargo, puede aparecer algún arco que aún no es entendido.
Otros
fenómenos de los arco iris
Además
de los efectos comunes de los arco iris hay muchos otros fenómenos
con los arco iris, alguno de los cuales se discuten a continuación.
Arco iris de
luz reflejada
 |
Rayos contribuyentes Figura 14
|
Así
como los rayos, que forman un arco iris directamente, es posible
formar un arco iris por rayos de luz indirectos. Una de las fuentes
principales de luz es la que produce la reflexión de una superficie
de agua, como de un lago o de un océano. La figura 14 muestra dos
gotas de lluvia, la primera contribuye al arco iris formado de rayos
directos del sol y la otra gota contribuye al arco iris formado por
rayos indirectos (el cual es reflejado de la superficie del agua). El
diagrama muestra que los rayos saliendo de ambas gotas a 42º de las
trayectorias a la cual entraron. Por consiguiente es claro que el
arco iris producido por la luz reflejada aparecerá mas alto en el
cielo, que la formada por la luz solar directa.
Arco iris
reflejados
 |
El arco iris reflejado Figura 15
|
Un
arco iris reflejado es un caso en que se puede ver un arco iris en el
cielo y simultáneamente ver su reflexión invertida en la
superficie del agua. La reflexión primero parece ser una reflexión
común ordinaria de un arco iris, pero no lo es. El problema vino a
luz en el siglo IXX cuando un artista exhibió una pintura con un
arco iris y su reflexión aparente en la superficie del agua.
Algunos declararon que no podría haber reflexión de un arco iris en
la superficie del agua, ellos estuvieron en lo cierto. Dijeron que el
artista estaba equivocado. La clave de esta aparente paradoja es la
referencia a como se forma un arco iris, y el hecho es que cada
observador ve un arco iris diferente, porque cada arco iris se forma
por un conjunto diferente de gotas de agua. El arco reflejado que el
artista vio no era la reflexión de un arco iris en el cielo, éste
fue formado simultáneamente en el cielo por un conjunto diferente de
gotas que fueron entonces reflejadas sobre la superficie del agua
hacia el artista (Figura 15).
Arco iris
lunar
El
sol no es la única fuente de luz capaz de producir arco iris, los
arco iris también pueden ser formados por la luz de la luna. La luz
de la luna es por supuesto más tenue que la luz del sol y de allí
que los arco iris formados por la luz de la luna no son tan
brillantes como los de la luz solar. La formación y la física de
este tipo de arco iris son idénticas a aquellas para los arco iris
formados por luz solar.
Experimentos
William
Livingston, un astrónomo solar especializado en fenómenos ópticos
atmosféricos sugiere lo siguiente: “rociando con una manguera se
pueden producir arcos supernumerarios visibles hasta el orden tres
“.
“Otra
forma es mirar una gota de agua de cerca, a unos dos centímetros
del ojo. Al ángulo del arco iris se alcanza a ver una porción
simpática de color".
Demostración del arco iris
Es
Difícil demostrar un arco iris en clase y casi imposible conseguir
la brillantez de uno visto al aire libre. La razón principal es que
solamente una fracción de luz pasa a través de la gota de agua o su
simulación y es reflejada para formar un rayo de arco iris. A pesar
de que el ángulo del arco iris puede demostrarse con láser, la
belleza total de todos los colores solo se muestra cuando se usa una
fuente de luz blanca (conteniendo todos estos colores). La luz del
sol es la mejor, por supuesto, pero la luz de una lámpara
incandescente cuya radiación para simular la luz solar (rayos
paralelos) puede ser usada con buenos resultados.
Como
ilustración aquí se sugiere dos demostraciones y un modelo de arco
iris.
Primera
demostración
(tomada de "Light
and Colour in the Open air"
de Minnaert
Si
se permite brillar a la luz solar a través de un agujero central en
una pieza de cartón blanco e ilumina un balón esférico, un arco
iris tenue aparecerá sobre el cartón. Con forma de
circunferencia y una distancia angular de alrededor de 42º, con el
rojo en el exterior como en el arco iris real. Si la parte posterior
del balón se pinta con pintura de plata o aluminio, la luz se
reflejará más y el arco iris será más brillante.
Segunda
demostración (tomada
de "Clouds in a
glass of Beer" de Bohren)
Él
sugiere usar un vaso lleno de agua que ha sido forrado con un espejo
flexible de película plástica aluminizada cubriendo la parte
posterior tal que la luz no se trasmita fuera. La luz viene de un
proyector de transparencias al cual se ha insertado una lámina opaca
con una rendija. El arco iris se ve sobre una pantalla.
Modelo
de arco iris
OBJETO:
Observar un arco iris circular casi completo usando un modelo hecho
con cuentas de vidrio.
DESCRIPCIÓN:
Se pegan las cuentas de vidrio a una pantalla negra para simular las
gotas de agua. Cuando esta pantalla se mira de cerca, con una fuente
de luz (puede ser el sol) viniendo de atrás del observador, se puede
ver el arco iris primario a un ángulo de cerca de 22º. El arco iris
secundario puede verse a un ángulo de cerca de 88.5º, y debe ser
visto mirando casi paralelo a la superficie de la pantalla, tal que
no puede verse al mismo tiempo que el arco iris de primer orden.
Varias
características de este arco iris son similares a las
características de un arco iris real: los colores están en el orden
correcto y son reales, el área fura del arco iris es muy oscura,
comparada con el área dentro del arco iris, y se pueden ver
fácilmente varios arcos supernumerarios.
El
arco real primario es de cerca de 41º, y el secundario es de cerca
de 52º. El índice de refracción mayor de las cuentas de vidrio
produce este desfase del arco iris primario a 22º y del secundario a
88,5º.
La
Fotografía mostrada fue tomada con una cámara de 35 mm usando una
lente gran angular de 20 mm. La cámara estuvo cerca de la fuente
puntual y al centro de la pantalla. Notar que el ángulo total del
arco iris es de unos 45º, mientras que el ángulo total de un arco
iris real es cercano a 90º.
EQUIPO:
Pantalla negra con cuentas de vidrio de 0,007" (0,18 mm) de
diámetro, una fuente de luz puntual brillante o luz solar.
CREDITOS
DE LAS FIGURAS USADAS:
Figura
3, 8, 10,12, 13, 14 y 15 Fuente: Greenler, R. Rainbows, Halos &
Glories
Figura
5 Fuente: The Usborne dictionary of science
Figura
6, 7. 9 Fuente: Hewitt, P. G. Conceptual Physics
Figura
11 Fuente: C. Boyer, The Rainbow from myth to mathematics
Figura
12,13 Fuente: Scientific American, July 1977























































